생성모델의 시초인 GAN. 생성 모델을 공부하기 위해서는 꼭 알아야 할 개념이기에 가장 기본적인 GAN에 대한 정리

Abstract

Generative model G와 discriminative model D를 사용해 두 가지 모델을 동시에 학습하는 generative model을 추정한다.
G : 입력 정보를 바탕으로 가상의 결과물을 만듦 (도둑)
D : G가 아닌 훈련 데이터에서 샘플이 나왔을 확률을 추정한다. (경찰)
G는 임의의 노이즈를 통해 훈련 데이터와 같은 분포의 가상 데이터를 생성하며 D는 해당 이미지가 생성된 이미지인지 훈련 데이터의 이미지인지 판단할 확률이 1/2가 될때까지 학습한다. (구별할 수 없음)
Introduction

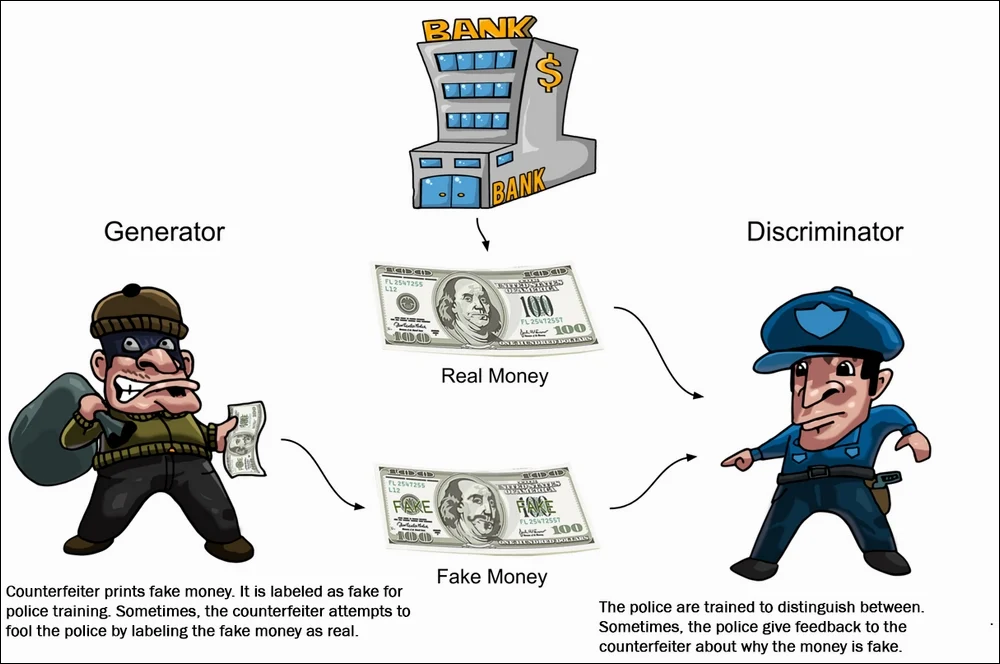
Generative model G 는 위조 지폐를 걸리지 않고 만든다고 치면, Discriminative model은 이를 잡아내기 위한 경찰과 같다. Discriminator 모델에서 generator에서 생성한 데이터가 실제 데이터에서 나온 '진짜' 이미지인지 G에서 임의의 분포를 따라서 만든 '가짜' 이미지인지 결정하는 법을 학습하며 Generator 모델에서는 학습을 거듭하며 더 진짜같은 이미지를 생성하게 된다. 이렇게 서로가 경쟁 관계로 학습을 하며 두 모델의 성능이 동시에 향상된다. 다층 퍼셉트론으로 구성된 두 모델이 경쟁하는 관계로 적대적(Adversarial) net이라는 이름을 붙였다.
Adversarial Nets

Adversarial Nets는 G와 D 모두 MLP 모델인 경우 가장 간단하게 적용할 수 있다.
먼저 generator의 분포를 학습하기 위해 input noise에 사전 분포인 \(p_{z}(z)\)를 정의한다. 이후 이 공간에 data space는 \(G(z;\theta_g)\)로 만들며 여기서의 G는 \(\theta_g\)를 parameter로 가지는 다층 퍼셉트론이다. 이후 이 샘플이 \(p_{g}\)가 아닌 실제 훈련 데이터셋에서 얻었을 확률을 계산하는 \(D(x;\theta_d\)를 정의한다.

이후 이 Adversarial net의 목적함수는 D와 G에 대해 D는 실제 데이터와 가짜 데이터에 대한 적절한 라벨링을 할 확률일 최대화한다. 한편 G는 \(log(1-D(G(z)))\)를 최소화 하도록 훈련한다.
위 식에서의 첫째 항이 D에 대해 x가 discriminator 모델에서 실제 데이터일 확률에 대한 로그를 취한 값이며, 두번째 항은 fake data z가 discriminator 모델에 들어갔을 때의 결과값을 1에서 뺀 결과이다.
D의 관점에서는 G의 가짜 데이터에 대해 0을, 실제 데이터에 대해 1을 출력해야 하므로 \(V(D,G)\)를 최대화 하기 위해선 목적 함수의 값을 0으로 만들어야 하며 G의 관점에서는 \(D(G(z))\)를 0으로 만들어 log0이 무한대 값으로 만들어 목적 함수의 값을 1으로 만들어야 한다.
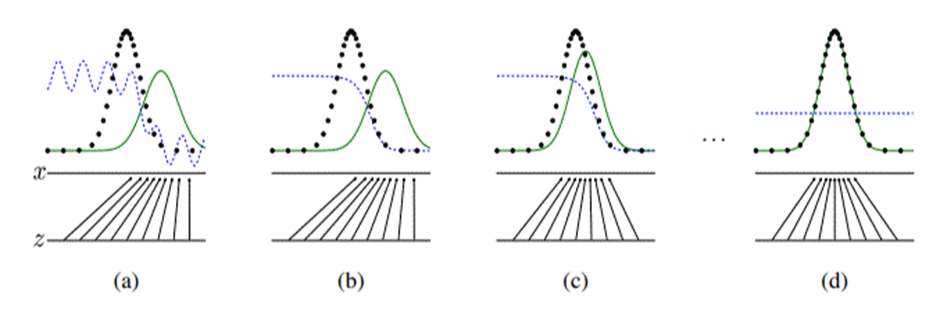
학습의 진행과정은 다음과 같다.
파란색 점선은 D의 조건부 확률 분포이며, 녹색 실선은 G의 생성 분포이다. 실제 데이터의 분포는 검은 점선으로 일정한 모양을 유지하며 하단의 실선들은 x와 z의 도메인에서 \(x = G(z)\)의 매핑에서 샘플들이 어떻게 generative distribution \(p_g\)를 나타내는지 보여준다.
(a) : 학습 초기
(b) : D의 분포가 데이터를 판별하고 있음
(c) : D의 학습이 이루어지면 G는 D가 판별하기 힘들도록 학습한다.
(d) 이 과정이 반복되면 G의 분포가 실제 데이터의 분포와 거의 비슷해져 두 모델이 더이상의 학습이 일어나지 않게 된다. (\(p_g = p_{data})\)
Theoretical Results
위의 minmax game이 제대로 이루어진다면 이론상 (\(p_g = p_{data}\)이며 논문의 알고리즘이 equation을 최적화하여 global optimum을 가져야 한다.

Generative Adversarial nets의 SGD 훈련 알고리즘.
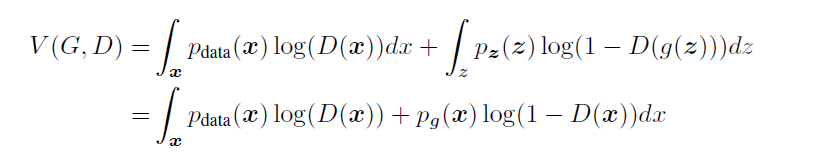
목적 함수인 V(D,G)는 V(G,D)에 대해 z를 샘플링 해 g(z)를 만드는 과정과 \(P_g\)를 따르는 x를 만드는 것이 같기 때문에
\(\int_{x}^{} \) 안으로 합칠 수 있다. 따라서 위와 같은 x에 대한 식이 나오며,
\(p_{data}(x) = a, p_{g}(x) = b, D(x) = y\)에서 alogy + blog(1-y)를 y로 미분한 값에 대해 0이 되어야 하므로

가 성립한다.

C(G)는 generator가 최소화하고자 하는 기준이 되며 이 식의 global optimal은 \(p_g = p_{data}\)일 때 만족한다.

여기서 D에 대한 max가 이루어진 D*에 대해서 위의 식을 가져오기 때문에 대입이 가능하며
log4를 더한 후 빼는 방법을 사용한다. log4 = log2 + log2이기 때문에

KL Divergence의 형태가 된다. 따라서
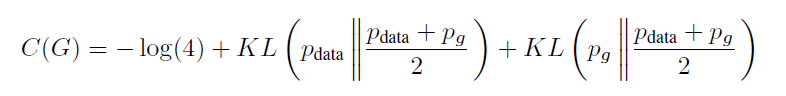
의 형식으로 변환이 가능하며, KL의 형태로 변환된다. 이후 JSD의 형태로 표현하면
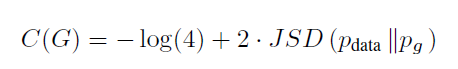
다음과 같이 정리되며 JSD는 0 이상이고 두 분포가 동일할 때 0을 가지므로
C* = -log(4)가 C(G)의 global minimum이며 C(G)을 min하는 최소의 값은 \(p_g = p_{data}\)인 경우가 유일해이다.
Experiments
MNIST, CIFAR-10, TFD에 대한 훈련으로
generator net에서 rectified linear & sigmoid를 사용하며 드롭아웃과 maxout activation을 사용한다.

Gaussian Parzen Window를 G에 의해 생성된 샘플들에 fitting 후 분포의 log - likelihood를 확인해 test data의 확률을 추정한 결과 다른 모델에 비해 경쟁력을 보인다.
Advantages and disadvantages
장점으로는 Markov chain등의 기법이 전혀 쓰이지 않고, 오직 backporpagation으로만 gradient 조정이 가능하다. 또한 학습에 inference가 필요하지 않고, 다양한 함수들이 모델에 접목될 수 있다. 이를 통해 데이터의 예시로부터 바로 업데이트되며 통계적인 이점을 가져올 수 있다. 하지만 단점으로는 D와 G에 대한 균형을 잘 맞추는 것이 중요하며 \(p_{g}(x)\)에 대한 명백한 대표값이 없다는 것이다.
Reference
https://arxiv.org/abs/1406.2661
Generative Adversarial Networks
We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that
arxiv.org
'논문리뷰' 카테고리의 다른 글
| Sign Language Transformer (2) | 2024.02.15 |
|---|---|
| Faster R-CNN (0) | 2023.12.23 |
| Attention Is All You Need (0) | 2023.04.24 |